ゆとり教育
戦後の詰め込み教育を反省して、ゆとり教育が叫ばれた時期がありました。そのとき、小数演算は難しいので円周と直径の比率は3.14…のところ、3で計算してもよいという通達があったと聞きました。
これでは誤差が大きいのではと気をもんでいましたが、ゆとり教育そのものがとん挫したようです。
乱数を用いて円周率を算出
乱数を用いて円周率を算出する資料は、山のように溢れていますが、仕組みを解説している記事は多くありません。今回、図を描いて丁寧に説明をします。
乱数の種類
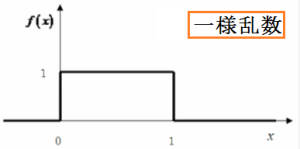乱数には、自然乱数、一様乱数、正規乱数などがありますが、ここではある有限の区間を区切って、その区間内で全ての実数が同じ確率(濃度)で現れるような乱数である一様乱数を採用します。
今回、JavaScriptを使ってプログラミングしますが、一様乱数はMath.random関数が用意されています。
算出の仕組み
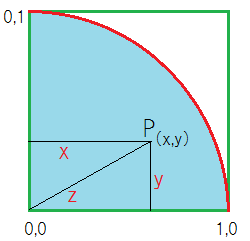一様乱数は0～1(0 <= r < 1)の区間で、同じ確率で発生します。一辺が１の正方形の中に2つの乱数を発生させ、xとyに割り振るとP点が求まります。
そのP点が1/4円の中に入る確率は正方形と1/4円の面積比であるπ/4になります。算出した確率を4倍すれば円周率が求まる仕掛けです。
P点が1/4円の中にあるかどうかは、xとyから半径zを求め、その値が1以下ならば円内にあると判断します。
正しくはx、yの二乗和の平方根の値を求めておく必要があるが、
の式が成り立つので平方根を求める必要はありません。
検証
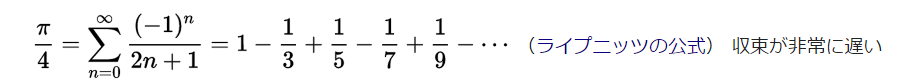
正確な円周率に近づけるにはMAXの値を大きくしますが、この方法で精度の高い円周率を求めることはできません。精度の高い円周率を算出するにはマクロリーン級数による近似値計算などがあります。
サンプルコード
<html>
<script type="text/javascript" charset="Shift_JIS">
// 乱数を用いて円周率を算出する
const MAX = 1000000;
var count = 0;
for(var i=0; i<MAX; ++i){
var x = Math.random();
var y = Math.random();
var z = x * x + y * y;
if(z < 1) ++count;
}
/* 円周率を計算・出力 */
var pi = count / MAX * 4;
alert("PI="+pi);
</script>
</html>
動作結果
さいごに
乱数を用いて円周率を算出してみました。紀元前2000年ころには古代バビロニアで22/7＝3.142857が使われていたといいます。なんぼなんでもπ≒3は暴挙としか思えません。