円周率の小歴史

円周と直径の比率は直径の大小に関わることなく一定であることは、人間の有史が始まってすぐに気が付いたことと思われます。

今から4000年も前に3、3.142857、3.125が円周率の近似値として使われていた記録が見つかっています。

円周率πは無理数であり小数点以下はここで終わりあるいはここからは循環するということはなく、正解に近づけるために近似値の桁数を増やすべく何千年にも亘り好事家の注目の的でした。

過去の記録を破ることは宝物を掘り当てることに近く、ライフワークとして多くの数学者のときめきを刺激したものと推測します。

外接円と内接円の間

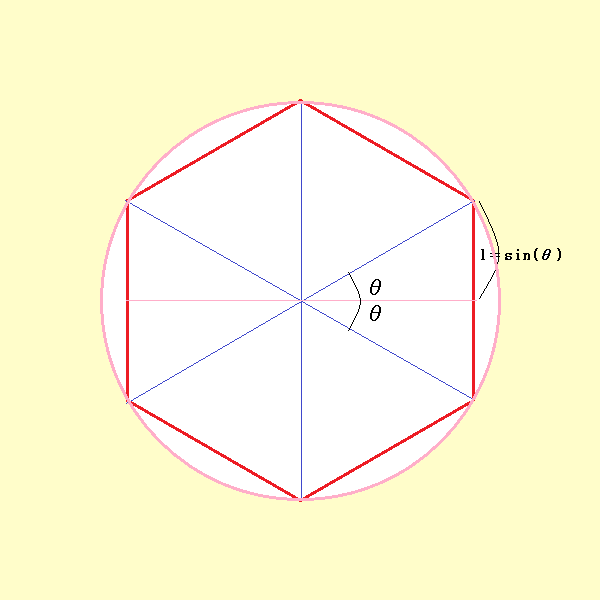
アルキメデスは多角形の外接円と内接円から円周率を求めました。6角形の外周は外接円直径のちょうど3倍です。多角形と近似値を表にしました。

頂点数を限りなく大きくすれば円に近づくことからより正確な近似値が得られそうです。

番号	頂点数	挟角の1/2	外周の長さ/直径
1	6	30	3
2	12	15	3.1058285
3	24	7.5	3.1326286
4	48	3.75	3.1393502
5	96	1.875	3.1410320

 

半径を1、頂点数をnにすると外周LはL=2*n*Sin(θ)で求められます。

 

年度の始まりにアルキメデスが考案した算出法で円周率を小数点以下5桁まで求めてみます。JavaScriptプログラミングコード付きです。

JavaScriptで円周率算出

次の画像をクリックしてスタートです。頂点数、ひとつの外辺からなる三角形の挟角、外周と外接円直径の比を表示し、3.14159を算出して終了します。

円周率算出の一方法

算出の簡便化

ここでは多角形を細分化した３角形の一辺の長さをMathのSin関数を使って求め、それを頂点数で乗じて算出しています。

Mathの三角関数は角度にラジアンを指定しますが度からラジアンに変換するときにMath.PIを使っています。

問いを用いて問いに答えています。アルキメデスは三角関数を使わずに√3を使っているようです。

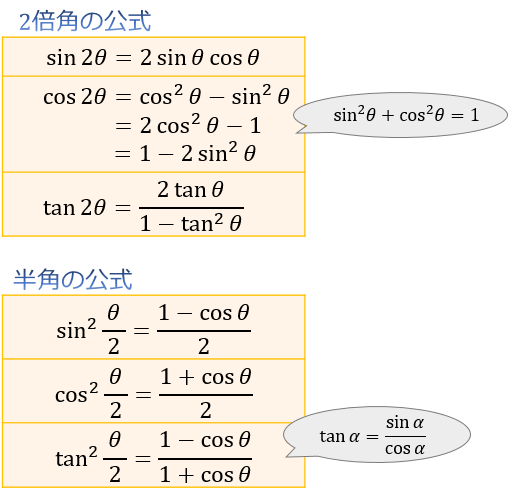
あとは半角の公式を使えば三角関数を使わずとも多角形の外周を求めることができます。だから間に合わせ的な方法ではありますが、問題ないと思われます。要は頂点数を多くすれば望ましい近似値にいくらでも近づけることができることを示しています。

ゆとり教育について

かつて小学校でゆとり教育が語られ、仮分数や帯分数、小数点を含む数値の四則演算を排除するために円周率を3で扱ってもよいといわれました。円の面積の算出式はπ・ｒ・ｒです。

半径を2乗してさらに円周率を乗じます。古代人の多くは半径を2乗して3を掛けて円の面積を求めていました。3は円周率の概略値です。外接円と内接円の間で述べていますが、3は6角形の外周です。円周率を3で代替することはかなりアバウトであり数学の歴史を4千年ほど戻すような振る舞いでした。

ゆとり教育のひずみが露呈して改善され胸をなでおろしている人がたくさんいるのではないでしょうか。

終わりに

円周率にまつわる話題は事欠きません。ある宴会で東海道五十三次の宿場名を延々と唱話する人がいてびっくりしていると、暗記した円周率を何十桁とあきれるほど叫び続ける人がいました。また、近代数学以前の話でしょうが、苦労して127桁まで計算し発表したところ、113桁にミスがあると指摘されたり悲喜こもごもです。

今は研究機関に勤めてなくても機能の高いコンピューターを利用できる時代であり、22兆桁、31.4兆桁など気の遠くなる桁数が発表されています。全数値を発表することもできないのではないでしょうか。

動きのある円周率算出法を表現する試みでしたが動きは地味でした。別の機会に再度、挑戦してみたいと考えています。

インドアの過ごし方

世界中で新型コロナウィルスが猛威をふるっています。外出して対面することがはばかられています。3つの密を避けるように要望されています。

おっつけ学校が再開するでしょうが、このまま五月連休明けまで休校になることもあり得ます。

屋内にじっと閉じこもるのは苦痛かもしれません。

これも試練のひとつと考え、開放的な行動をいっとき封じて自宅学習などインターネットを利用した研究的な生活に切り替えてみませんか。