月別アーカイブ: 2022年3月

ナンプレ（二国同盟）

ものづくり筆耕ブログ






ナンバープレイス

ナンプレ（数独）研究©2022 TacM, Ver0.03

通算記述内容

➊ナンプレの入り口

❷解法のあらまし

❸単一候補検出(single candidate)

❹隠れシングル(Hidden Singles)

❺二国同盟(Naked Pairs)

❻隠れ二国同盟(Hidden Pairs)

⑦ポインティングペア(Pointing Pairs)


ナンプレの効果

当サイトのナンプレに関する掲載は脳トレーニングの一環としてプログラミング学習と合わせ論理的な考えを育むものです。

社会生活をする上で他人にわかりやすく物事を説明することが要求されます。それには日頃から脳を刺激し鍛錬することが大切です。

脳の内部細胞を磨くことによって頭の切れが良くなります。楽しみながらナンプレに挑戦してみましょう。

おさらい

今までにコンピュータを使ってナンプレの自動解答を求めるためのシステム構築として掲載してきた全体の流れを示します。冒頭の大目次に表したように、ナンプレの概要から始まり解法のあらましと代表的な解法の解析を述べています。

マスの位置を表示する方法など順を追って読んでいただくと理解しやすいでしょう。では二国同盟(Naked Pairs)と隠れ二国同盟(Hidden Pairs)について見ていきます。

❺二国同盟(Naked Pairs)

前回までの流れを踏襲し、ナンプレの解法に進みます。ナンプレを解くに当たり、状況に応じて適切な解法を採用しなければなりません。今回は二国同盟と呼ばれる解法です。

 

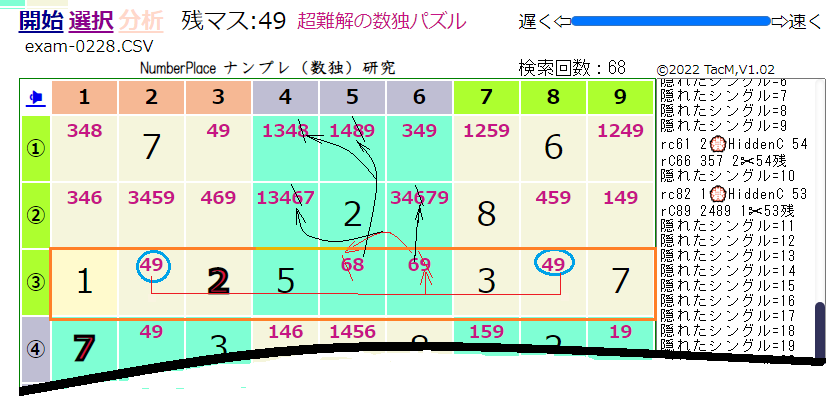
上の図において、大きなサイズの黒い数字は問題として与えられ、小さな赤い数字はナンプレルールに基づいた候補数です。図により具体例で説明します。オレンジ色に囲まれた3行目に注目すると、RC32とRC38に49の候補数が挙げられています。49は3行の他のマスには存在せず、二国同盟が成立しています。

『二国同盟(ネイキッドペア, Naked Pairs)とは2つのマスに限定された2つの候補があるとき、その同一グループの他のマスにある二国同盟が成立した候補は削除できる』という解法です。

これを上の図に当てはめると3行目の9マスにおいて、49はRC32とRC38以外には使うことができません。よって、3行の他のマスから4あるいは9を削除することができます。RC36の69から9を削除し、RC36に6を確定させます。RC36確定を反映してRC35の68から6を削除するとRC35は8が確定します。

一方、ブロック2に着目すると、6と8が確定したことにより、RC14と15から8，RC24と26から6を削除することができます。他に5列と6列から8と6を削除できますが、4行から9行までの下部分をざっくり削除したので省略します。

二国同盟解法

二国同盟の解法は図に示した候補数の制御を行列ブロックのすべてについて確認します。

二国同盟による候補数の制御は、9行9列9ブロックに3重に絡んでいるので動的にその後の確認に反映させなければなりません。




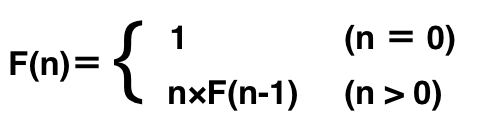
再帰処理の代表例《階乗を求める関数》


そのため、再帰処理が可能ならば一般的な処理よりも簡潔なコードで制御を実現することが可能です。再帰処理は上図に示した階乗を求める関数が代表例として有名です。再帰処理に注目するとこれからの進み方がはかどるでしょう。

❻隠れ二国同盟(Hidden Pairs)

隠れ二国同盟(Hidden Pairs)とは、 「2つのマスに限定された2つの候補が他の候補と同居する時、 そのマスの他の候補を削除できる」です。隠れ二国同盟は、その2つの候補が行(または列、ブロック)の中で2度だけ出現しています。隠れ二国同盟からそのマスの他の候補を削除して正真正銘の二国同盟に帰着させて同様の制御を行います。

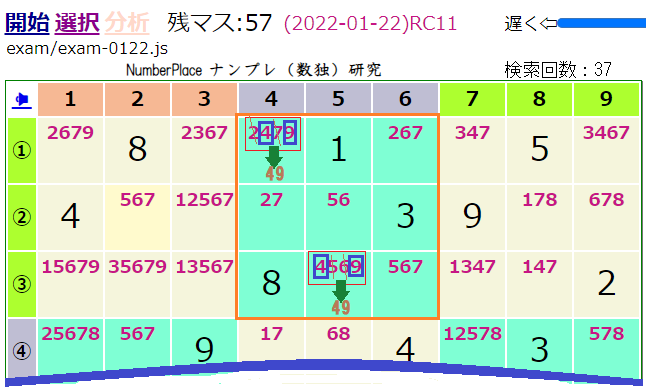
隠れ二国同盟解法

上図のオレンジ色に囲まれたブロック2に注目すると49の候補数は9マスの内、RC14とRC35の中で限定的に使われています。このような状態を隠れ二国同盟が成立していると表現します。

隠れ二国同盟のルールでは同盟成立として選ばれた2つの候補以外の候補を削除できるので成立要因の候補数だけをそのマスに残します。

この解法として2候補による隠れ同盟を速やかにあぶりだすことです。

以下の図は400数十年前、戦国時代の同盟関係を示しています。ナンプレとは何ら関係ありませんが頭休めです。

「武田信玄の歴史を年表・勢力図で簡単に、ざっくりと見てみよう！」より

動作例と操作方法

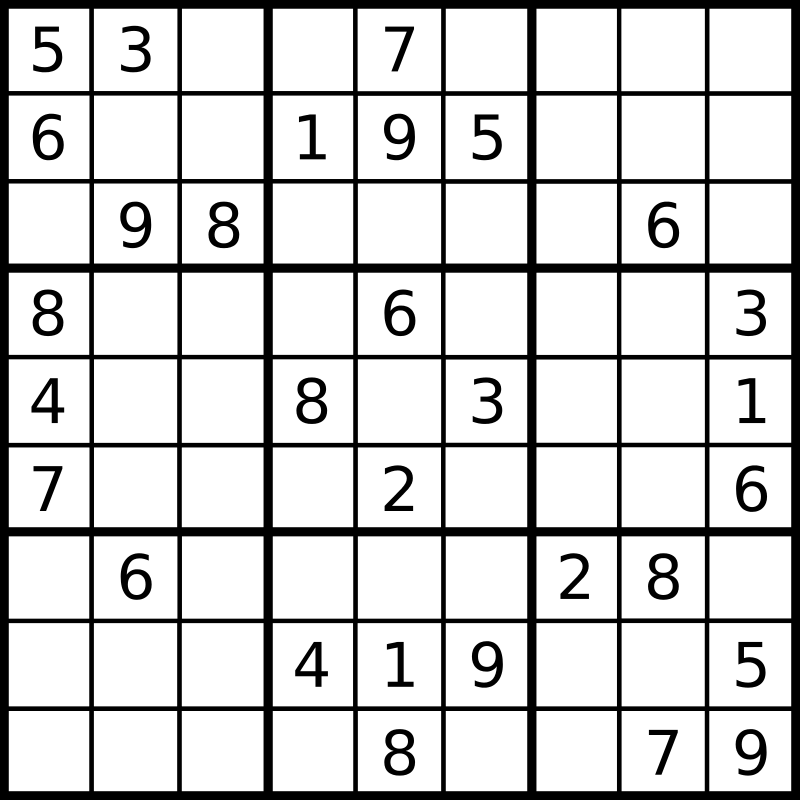
下図に二国同盟、隠れ二国同盟を用いてナンプレ課題を解いています。当初、初期画面が表示されています。開始ボタンをクリックすると9×9のマスが少しずつ埋め込まれます。右上の動作中ボタンが回転中から静止すれば終了です。

右端できごと欄のよくできましたマーク（💮）の後、’Allian’が出力されています。これが二国同盟、隠れ二国同盟解法によって確定した数字であることを表しています。

動作例



あとがき

二国同盟と隠れ二国同盟は行・列・ブロック内の2つのペアにより、限定される柵（しがらみ）を利用して正解を絞る方法でした。

単一候補(single candidate)と隠れシングル(Hidden Singles)よりは幾分、難しくなっています。これらが大過なく組み込み成功なれば先は明るいと言えましょう。

ポインティングペア(Pointing Pairs)

次はポインティングペア(Pointing Pairs)解法を取り上げる予定です。

coming soon! 🔜

おまけ

2023年度から高校において「情報Ⅱ」がスタートします。当サイトはそれらと連動しているわけではありません。何はともあれ論理的な考えを育むために存在します。

再帰関数に遅延処理を導入

ものづくり筆耕ブログ

同期処理をどこに入れるか

この記事は前回からの続きです。再帰関数factorialは1行で定義できます。同期を可能にするコードをこの関数に入れるのは難解です。幸い、同期をサポートする仕組みが仕様として確立されました。新設された仕様を応用した例を前回、掲載しました。

 

内容的には前回と同じですが説明を図にしました。再帰関数に遅延処理を加える方法の一つとして参考になりましたらありがたいです。

実行例

ブラウザの再ロードボタンを押して再実行できます。


 
 
 
 
 
 
 
 
 
 
 
 
 




 

サンプルコード

<html>
<Div style="float:left; width:216px; height:560px; font-size:22px; border:1px solid blue;">
<div id="fact01" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact02" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact03" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact04" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact05" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact06" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact07" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact08" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact09" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact10" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact11" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact12" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
<div id="fact13" style="width:210px; height:40px; margin-top:4px;">&nbsp;</div>
</Div>
<Div style="float:left; margin-left:34px"><img src="https://aidesign.lolipop.jp/wp-content/uploads/2022/03/myAsync.png" width=350" height="560"></Div>
<script type="text/javascript" charset="utf-8">
myAsync();							//main関数呼び出し

async function myAsync(){			//非同期関数を定義する際にasyncをつけて宣言する
  for(var i=1; i<=13; ++i){
	var id="fact"+("0"+i).slice(-2);
	var result = await myPromise(i);//実行結果を待つためにawaitをつけて実行
	document.getElementById(id).innerHTML += (" "+i).slice(-2)+"!= "+result;// 1 2 6 24 120 720
  }
}
function myPromise(num){			//非同期な処理をする核となる関数myPromise
	return new Promise(function(resolve) {
	  setTimeout(function(){resolve(factorial(num))},1000)//1秒のディレー後にresolve起動
	});
}
function factorial(n) {				//階乗を求めるrecursiveな関数
   return (n<=1) ? 1 : n * factorial(n - 1);
}
</script>
</html>

 

ディレー処理の一例

ものづくり筆耕ブログ

目にも留まらぬ早業

動きが速すぎて何が起きたのか判らないときがあります。映像の世界ではスローモーションビデオによる再生で動作をゆっくり見せています。プログラミングではwait, sleep, delay等の関数が用意されているのでゆったりした表現を支援しています。

そのあたりは『同期的な表現』で取り上げました。今回、再帰処理(recursive processing)で遅延するにはどのように制御するのか少し戸惑いましたので、確認した一例を記録に残します。

再帰処理(recursive processing)





再帰関数(recursive function)の代表例に階乗(factorial)関数があります。関数の最後でディレー時間を設けるに当たりどこにディレー処理を用意すればよいのか悩みました。

求める階乗の値に関わらず一律に同じ待機時間に設定するにはそう簡単ではありません。待機時間を設置するには、setTimeout, setInterval, Promise, async/awaitなどがありますが、ここではasync/awaitを使っています。

async/awaitはPromise関数の標準的な使い方を短かい記述で可能にした表現方法のようです。

次のような使い方でC言語のsleep関数相当の機能を実現できます。非同期処理はasyncをつけた関数内でawaitをつけて実行させます。

階乗を求めるrecursiveな関数factorial()はmyPromise()のスコープ内に定義されていますが、必ずしもスコープ内に置く必要はありません。実質的にawaitをつけた関数で実行されれば期待した動作になります。

動作例

１～6の階乗を1秒間隔で表示します。ブラウザの再ロードボタンにて何度でも実行できます。

myAsync is starting.  


ディレーを実現する関数のサンプルコード

<html>
<script type="text/javascript" charset="utf-8">
const CRLF="<BR>";
myAsync();

async function myAsync(){				//非同期関数を定義する際にasyncをつけて宣言する
  for(var i=1; i<=6; ++i){
	var result = await myPromise(i);	//実行結果を待つためにawaitをつけて実行
	if(i==1) document.write("myAsync is starting."+CRLF);
	document.write(i+"!= "+result+CRLF);// 1 2 6 24 120 720
  }
}
function myPromise(num){				//delay 1秒
	return new Promise(function(resolve) {
	  setTimeout(function() { resolve(factorial(num)) }, 1000)
	});
 function factorial(n) {				//階乗を求めるrecursiveな関数
  if(n<=1)	return 1;
  else		return n * factorial(n - 1);
 }
}
</script>
</html>

他人の出世

ものづくり筆耕ブログ

関係度による

妬み（ねたみ）

古今東西、老若男女を問わず他人（ひと）が出世すると複雑な思いに駆られます。

人は多くの煩悩を抱えていて妬みや嫉みから脱却するのは至難です。どんな賢人であろうと嫉妬心と無縁とは言い切れまい。

それはその人と自分との関係度や出世の度合いによって決まったパターンに分けられます。

恥を忍んで自分の経験や身近な人の対応をまとめてみます。まず、出世する人の力量が自分と大差ないと考えられる場合は穏やかではありません。

それに隣人、同僚、同級生がワンランク上昇気流に乗ったときも複雑な思いが交錯します。

自分の年収が500万円で同レベルだった知り合いが600万円の年収を得る出世を遂げることはかなりのショックでしょう。大差の額たとえば1500万円ですと嫉妬の度合いは低く大きなショックはないでしょう。自分よりちょっと高額が一番、いまいましいのです。

時代によりけり

氏より育ちという言葉もあります。人々が自由闊達に思い描いた人生を歩める時代は妬み心も少ないでしょう。私の幼少期は今ほどモノに恵まれた時代ではありませんでした。底意地の悪いいじめや嫉妬心は少なかったですが、他人への悋気は日常茶飯事でした。他人が出世したり新しい世界に踏み出してもなかなか、認めたがらないのが常でした。

婿は一生、婿

半世紀も前の話ですが、婿にいった者は一生、「〇〇家の婿」と言われ続けました。地方の市役所に勤め一人娘と結婚し、やがて課長に昇っても近隣の人々は婿と呼んでいました。

婿に行った目端（めはし）がきく後輩がいて、『行った先が遠縁で同姓だから行ったんだよ』と語っていました。別の話ですが、やりて奥さんがクリーニング取次店を開業し成功を収めて立派な洋装店に衣替えしても口さがない人々は「洗濯屋のおばさん」と長年、旧称を使っていました。

出世の階段（愛宕神社）

相撲協会はそれなりに出世した力士が引退すると親方と呼ばれる役職に付かせ、地方巡業会場の整理やテレビ解説をする習わしがあります。親方株を取得して「〇〇親方」と呼ばれるほかに、現役時の地位で「元大関〇〇龍、元前頭3枚目△△山」などと呼称されます。

古い時代、現役時の四股名と地位を紹介するとき、ある時から引退時の地位から最高位で呼ぶように改められました。大関まで昇進しケガをして成績が振るわなくなり十両に落ちて引退した場合でも元大関と名乗ることができます。晩年は番付が下がることが多いです。最高位を名乗る決まり事は優しさのある計らいといえましょう。

「△△家の婿」よりは「〇〇市役所厚生課長」の方が通りがよく、その人の評価が平均点以上かどうかにかかわらず最高位で呼んであげたいものです。民度と言えば麻生元総理大臣が思い起こされますが、民度には優しさが含まれているものです。

最後に

妬（ねた）み、嫉（そね）みなど漢字で書くと女へんが多いです。女性には男にできないことをやってのけるものがあります。

男性は女性の力を恐れてこのような字を当てたのでしょうか。時間があったらここら辺りを深掘りしたいものです。

人物評価

ものづくり筆耕ブログ

時代背景により変化

歴史上の人物評価は時代時代により評価が異なります。多くは時代背景が影響しています。

私の幼少のころ、徳川家康はタヌキおやじなどと辛らつ評価され続けました。

山岡荘八の『徳川家康』が映画、TVドラマ化したあたりから評価が上がったと記憶しています。

家康は幼少期を人質として過ごし我慢強い豊潤な性格を形成させ、戦乱を終結させた傑物へと評価を変えました。

一方、ここ20～30年、源義経の評価が最低になっているように感じます。義経は歌舞伎演目『勧進帳』で取り上げられるほどに国民的人気が高かったのに時代の流れでしょうか。

安定した世情においては革命児や動乱の英雄よりも頼朝のようなまとめ役が好まれます。

しかし、日本三大悪女の日野富子の評判はあまり変わってないようです。一度、三田佳子の主演『花の乱』でNHK大河ドラマで取り上げられましたが知名度がいまいちであり、話題性に乏しいです。

史上最大の無為無策な作戦と酷評される太平洋戦争終盤インパール作戦の責任者は、自身や家族・子孫の保身・名誉のために、国会図書館に録音証言を残しています。歴史研究好きな方には一度覗いてみてはいかがでしょう。

戦争の評価は最低100年かかることが定番です。

愚かな企みは慎まなければなりませんが、起きてしまったことは100年かけて挽回するしかないでしょう。

人のうわさも100年たてば変わるというむか～しからの言い伝えでした。

春の兆し2022

ものづくり筆耕ブログ

弥生

寅年がやってきたと思っていたのにもう弥生三月です。今般、スーツを着る機会があり、ネクタイを締め久方ぶりに電車に乗りました。

お気に入りの一張羅（いっちょうら）は長く、箪笥の肥やしでしたのでやっと日の目を見た感じです。ネクタイの結び方も忘れるほどで脳にはよい刺激になりました。

着るものに掛ける予算はなくなり、状況に応じた役割に変えています。スーツ用替えズボンは必要なくなりもったいないですが散歩用に再利用しています。初めは場違いな雰囲気も自然な環境になじんできます。着こなすのもその人のアイデア、勇気、センス、技量でしょう。

人まね文化からの脱却

この頃の電車内では100%、スマホいじりの風景で埋め尽くされていましたが、今回、20代の女性が「コンピュータープログラミング言語『HTML』」という解説書を読んでいるのを見かけました。

スマホやタブレットなどの携帯情報端末で動作するシステム開発というよりも一般教養として読んでいるようでした。

HTMLをこよなく愛して自ら情報を発信され新しい風を吹き込んでもらいたいです。将来を担う若者によって人まね文化からの脱却が進むことを願っています。

 

「うれしいひな祭り」