交差数判定
数回にわたり、日本地図上をクリックしてヒットした都道府県に紐づけられた情報を扱う例を取り上げてきました。今回、地図上のピンポイント位置情報の代わりに、動的に変動する位置情報が多角形の閉空間の内にあるか外にあるかを判定する状況を図示化しました。
 指定されたポイントが領域の中に存在するかどうかを判定するのは簡単ではありません。主要なアルゴリズムが2つあります。
指定されたポイントが領域の中に存在するかどうかを判定するのは簡単ではありません。主要なアルゴリズムが2つあります。
- Crossing Number Algorithm
- Winding Number Algorithm
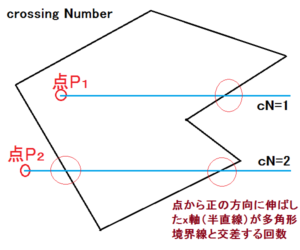
今までCrossing Number Algorithmを追いかけてきました。点から正の方向に伸ばしたx軸(半直線)が多角形境界線と交差する回数を数える方式(crossing Number Algorithm)は、この回数が奇数ならば、その点は多角形の内側にあり、偶数ならば外側にあると判定するアルゴリズムです。
これまで、画面上に映し出された地図上を指定した点について内外判定してましたが、今回は福岡県に見立てた8角形の周りを一周するとき、その位置により内に存在するか外に存在するか何回か状態変化します。その状況を図示化しています。
動作例
動作は8多角形の周りを半時計方向に円状に移動する点がエリア内にあるか外にあるかを随時表示するものです。外にあると判断されたら白色ではずれと、内にあると判断されたらマゼンタ色でヒットと表示されます。はじめボタンを押下して開始です。
中核の内外判定関数
const poly=[130,44, 432,44, 432,343, 232,343, 232,400, 40,400, 40,190, 130,190]; //Array
function pointInPolygon(px, py, Array){ // <<<<< 点の多角形に対する内外判定関数 >>>>> Array:poly 県の形:4 6 8角形 11 15 19
var l=Array.length; // console.log("L", l);//stop20();
var cN=0; // cNが奇数ならば点Pは多角形Tの内側に、偶数ならば外側にあると判定
for(var i=l-2,j=0,yi,yj,cW; i>=0; j=i,i-=2){// Arrayテーブルの大きさ:i:14
yi=Array[i+1]-py; // role-1:上向きの辺。点Pがy軸方向について、始点と終点の間にある。15
yj=Array[j+1]-py; // role-2:下向きの辺。点Pがy軸方向について、始点と終点の間にある。1
if((yi>0)!=(yj>0)&&(cW=sign(yj,yi)) == sign(yj*(Array[i]-px), yi*(Array[j]-px))) cN+=cW; // 判定
} // role-3:ルール1,ルール2を確認することで、ルール3も確認できる。
var r = (Math.abs(cN) % 2) == 1; // role-4:辺は点pよりも右側にある。
return r; // true false
} // ray casting algorithm, cN:crossingNumber, cW:counterClockwise
function sign(a, b){return (a > b) ? 1 : (a < b) ? -1 : 0;} // 両者を比較して、-1 0 1を返す
応用例
内外判定は北緯35度上に位置する県名をすべてあげるのに応用することができそうです。
このような例は静的な利用で既に簡単に解決する方法が他にありますが、次のような動的な使い方は貴重です。
自分がこれまでに住んだ県を順に選択する情報をパスワードにすることに応用することができます。

