最大公約数とは

最大公約数とは、複数の整数において共通する約数の中で一番大きい数のことを言います。前回の最小公倍数は対象となる数を整数倍したときの現象を考えましたが、今回は数を構成している約数について考えます。

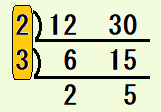最大公約数を筆算で求めるには、共に割り切れる数で割っていき割れなくなるまで繰り返して、割り算に用いた除数の積が求める値になります。12と30の最大公約数を求める例を左に挙げました。

ここではそれぞれ対象となる約数の中から抽出した共通の約数のうち、もっとも大きな数を最大公約数とする方法を図で説明します。

ユークリッド互除法による算出

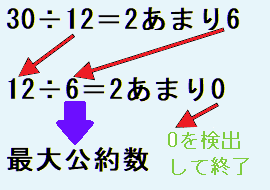値が大きな数の最大公約数を求めるとき、ユークリッドの互除法が便利です。

図に示したように2つの数で割り算をし、前回の除数を余りで割ることを繰り返し、余りが0になるまで続けて最後の除数を最大公約数とする方法です。

最大公約数の実際例

日常生活において、最大公約数は複数の立場の中でどちらにも通用するような状況にあるとき、最大限の効果を生むような場合に使われることがあります。ここでは12と30の塊があり、2つの塊でなるべく大きな塊に分割するする例を考えてみます。

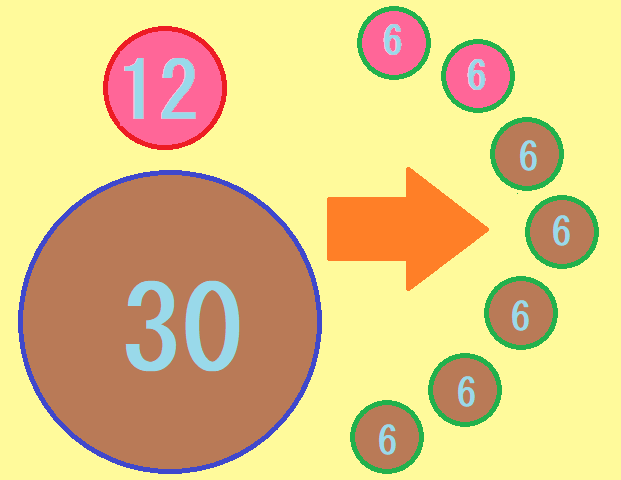
両者は偶数であり、2ずつまとめると前者は６、後者は15のグループになります。3でも分割できます。もっと大きな6はどうかというとこれも問題ありません。30の塊はまだ余裕がありますが、12の塊では6が限界です。この辺りで手を打つことになるでしょう。

このように最大公約数は2つの塊を同一の数で等分割する際、なるべく大きい数を割り当てる問題にたとえられます。最大公約数を図で理解してみましょう。

最大公約数を動的表示する

最大公約数を動的表示するには下のメニューの中から●の付いた項目を順にクリックして最大公約数の意味を理解しましょう。再試行の際はブラウザの↻再読み込みボタンをクリックします。

 

 

庶民の幸せのひとつ

海外旅行に出かけ豪華レストランで食事をして、ブランド品を土産に買うばかりが最高の幸福とは限りません。

散歩の帰りに心やさしい家族が買ってきた品のよい和菓子を、とっておきのお茶でいただくのは庶民の最大公約数的幸福と言えるのではないでしょうか。