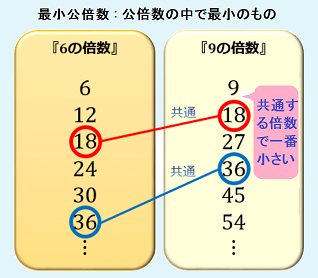
最小公倍数とは

最小公倍数(LCM, Least Common Multiple)は、2つ以上の整数の公倍数のなかで最小の自然数を言います。日常のなかで最小公倍数ほど生活に根付いている数はありません。

最小公倍数の卑近な例として複数の食材を等間隔で配給することを考えます。食材Aを3日ごと、食材Bを4日ごとに規則正しく配給し続けると12日後に同じ日になります。このようなケースは至る所で経験するでしょう。

洗濯は2日に一度、室内清掃を3日に一度の割合でし続けると6日ごとに両方することになります。それらを図にしてみました。数に親しみを感じながら算数、数学に取り組みましょう。

規則を図示化する

年中無休のスポーツジムにAさんは4日ごとにBさんは3日ごとに出かける場合を想定しました。

ジムに通う間隔を細線による円の大きさで表し、赤と青の小円でメンバーを図にしています。間隔が大きければ円の径も大きくなります。

2つの色付き円が接したときに、二人の訪問日が同一になって出会うことになります。開始ボタンをクリックすると二人はジムに通い始めます。

開始最小公倍数の研究

細線円の回転は時間の経過を表し、歯車の原理に基づいて両円は逆回転します。円Aは4日、円Bは3日で一回転する様を模しています。12日目に円Aが3回転、円Bが4回転したときに両者は出会います。このときの経過日が最小公倍数に匹敵します。

下の直線は時間スケールを横軸にしています。上部メンバーA, B 色付き円が再び横線上の元の位置に来た時がジムの訪問日でありスケール上に表示されます。

図に示した動作は最小公倍数が決定したところで終了していますが、以下に少し長めの結果を表示します。

最小公倍数を図示してみました。初めての試みで思うような結果を残せませんでした。もう少し研究します。