3と4と8の最小公倍数

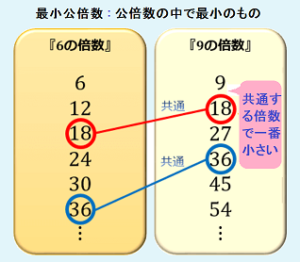最小公倍数とは複数の数の倍数（公倍数）のうち最小の数を指します。3の倍数は3, 6, 9, 12, 15…であり、4の倍数は4, 8, 12, 16…です。このことから3と4の最小公倍数は12です。

これらの事象は実際の生活にも当てはまります。たとえば3日ごと4日ごとに繰り返される放送が次に同一日に放送される事例や年中無休の病院に3日ごと4日ごとに通院して再び患者同士が出会う出来事などにたとえることができます。

スポーツジムに通う事例

対象数が2から3になっても考え方は同じです。今回、一定間隔でスポーツジムを利用する3人がスポーツジムで一緒になって次に出会う日を例に最小公倍数を図で解説します。

エアロバイクで体を鍛えている三浦さんは3日ごと、鉄棒を得意とする四元さんは4日ごと、ランニングマシンを利用する八木さんは8日ごとにスポーツジムに通っています。

では3者が次に一緒になる日を考察します。

現象を図にし動作を下の図で説明します。

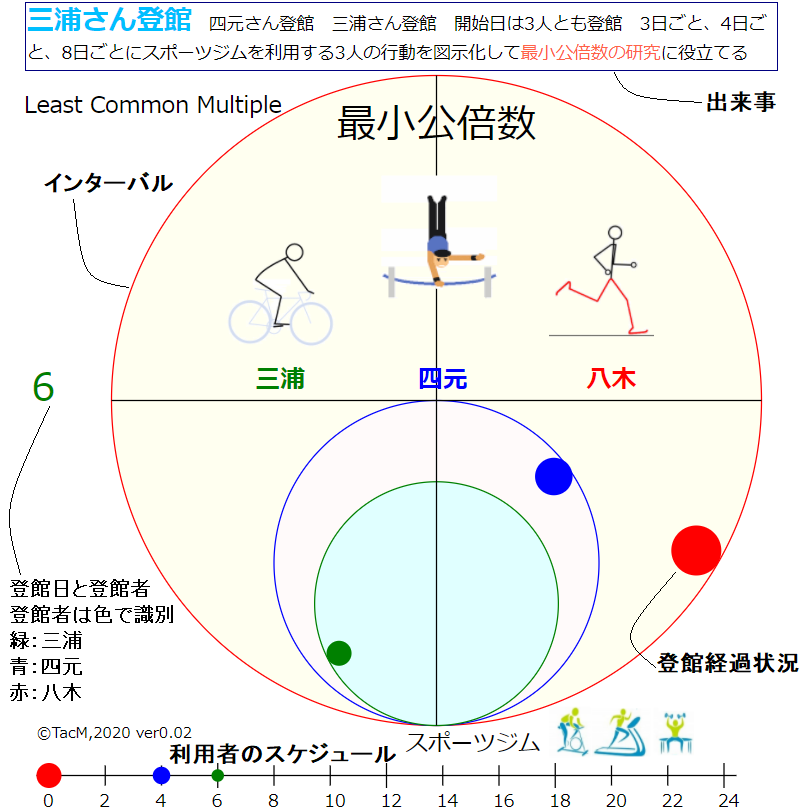
3つの大きな円は一周の長さで次に訪れるまでの間隔（所要日数、インターバル）を示し、大きな円は小さな円よりもインターバルが長いことを意味します。

円周長は半径の２π倍だから描く円の半径をそれぞれ3：4：8の比率に設定しています。緑、青、赤色の中くらいの円によりジム利用者の登館経過を表示しています。

大円の最下部にスポーツジムが位置しています。出来事は右上に表示され、利用者の行動は図の最下部に示されます。3つの動く絵はスポーツジムの中におけるトレーニング姿を表現しています。

3,4,8の倍数について

ジムに通館する間隔をひとつの数になぞらえ、3者に共通する数が初めて現れたときが最小公倍数とみなすことが妥当です。最下部の目盛り付き直線が経過日数を示し、登館時に利用者に見立てた小円が一気に移動します。

インターバルの状況を表示する中円や小円が3つとも重なった時が3人が出会ったことを意味し、最小公倍数の現象が出現しました。このまま続ければ24日後にまた再会します。

動作例

ページのロード後に自動スタートするので再実行するにはブラウザの再読み込み（🔄）ボタンをクリックします。

3, 4, 8の最小公倍数