ライプニッツの公式により円周率を算出
前回、乱数を用いて円周率を求めました。精度の高い円周率を求める方法は乱数を用いません。「乱数を用いて円周率を求められますよ」ということを図を使って解説してあります。
一様にばらつく乱数を使うことが基本で、偏った乱数では実態に即した円周率は求まりません。一般に乱数関数は言語処理系が持っているので精度の高い円周率を求めるには他力本願にならざるを得ません。
自力本願による解決
円周率を求める無限級数の近似式はたくさんあります。近似式は規則性があり、繰り返し処理で算出可能です。小さい繰り返し回数で精度の高い値を求めることを収束が速い算出法と表現します。収束が速くはありませんが、式がシンプルで有名なライプニッツの公式があります。
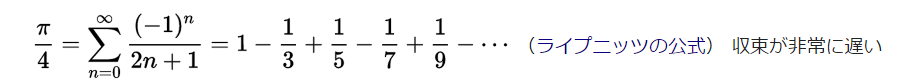
総和記号の式を大きく明示すると以下の図のようになります。
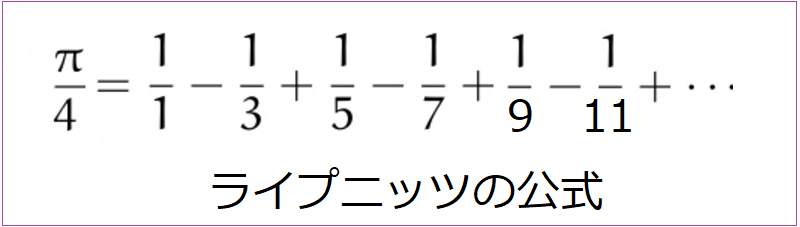
今回はこれを使って円周率を求めてみます。古くはFORTRAN、BASIC、Cなどで取り上げられていますのでJavaScriptで記述したプログラミングコードを解説します。
プログラミングコード
<html>
<script type="text/javascript" charset="Shift_JIS">
// ライプニッツの公式を用いて円周率を算出する
const MAX = 50000; //繰り返し回数
const DIFFERENCE = (0.0001/4); //差分による収束判定値
var pi4 = 0; //円周率格納変数
var previous = 0; //直前の計算値
var delta; //差分
for(var n=1; n<MAX; n+=2){ //1, 3, 5, 7, 9, 11, 13
pi4 -= (n % 4 - 2) / n; //
delta = previous - pi4;
//console.log("N="+n+" PI="+(pi4*4)+" deleta="+delta); /* 円周率を計算・出力(解析用) */
if(Math.abs(delta) < DIFFERENCE) break; /* 収束 */
previous = pi4;
}
document.write("N="+n+" PI="+(pi4*4)+" delta="+delta); /* 円周率を計算・出力 */
</script>
</html>
上の図に示した公式をJavaScriptでプログラミングしています。
ライプニッツの公式を凝視すると、各項の分子は1でその符号は正、負が交互に現れます。分母は初期値が1で、等差2の等差数列であることが分かります。このことからすると、繰り返しインデックスは1から始まり、増加値が2であることが望ましいと言えます。
11: pi4 -= (n % 4 – 2) / n; //pi4+= (2-(n % 4)) / n;
上の式は総和記号を実現させる式の肝部分です。総和記号を厳密に解釈すると右のような表現になるが、演算順序を変えると左のように少し単純化できます。
10行目のfor文で制御変数の初期値を1に、増分を2にしてあります。14行目であらかじめ設定した収束値になったかどうかを判断しています。
動作結果から
収束の速い近似式による収束のありさまを下図に示します。200回ほどの繰り返し回数で精度の良い円周率が求まっています。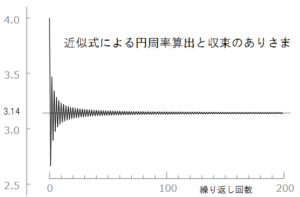 今回の動作結果から判断すると、仮に設定した収束値が得られるまで20000回かかりました。やはり、収束が遅いことが明らかになりました。
今回の動作結果から判断すると、仮に設定した収束値が得られるまで20000回かかりました。やはり、収束が遅いことが明らかになりました。3.1416まで算出するにはかなりの繰り返しが必要になります。

ライプニッツの公式は単純な規則性があり、サンプルとして取り上げられますが、円周率算出の本命とは言い難く、その席はマチンの公式などに譲ることになります。